These harmonics interact and interfere with each other in a complex process of phase summing and cancelling to a single overall complex pattern of vibration that contains all the individual harmonics.
Sound created in nature are very complex. We can use an oscillator to create less complex waves but even relatively simple waves, such as a square wave, are many times more complex than a sine wave.
Now either read on below, or watch our sister site's (www.projectstudiohandbook.com) video on Complex sounds here ..
Decoding harmonics in the brain
One of the wonders of nature is the human brains ability to de-construct a complex wave, hear all the individual harmonics, and identify the source sound.
So when we listen to a single sound, such as a snare drum, the brain recognises it from its unique combination of harmonics.
But the brain can also decode all the harmonics of all the individual sounds we hear in a completed mix, thus allowing us to identify the individual instruments. It's truly amazing that so much information can be carried in a single pattern of changing air pressure energy, and de-constructed by the brain.
How a square wave is created
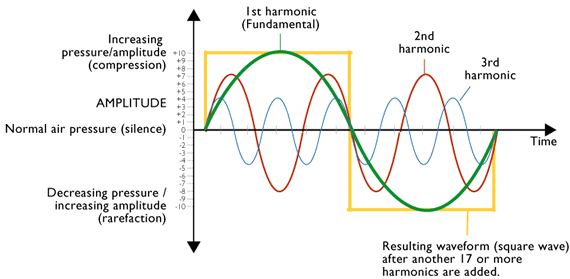
To illustrate how harmonics combine to create a complex wave, it is practical to use the example of the square wave. The diagram below shows some (3) of the individual harmonics required to create a square wave (you actually need at least 20 harmonics to approach a squareish shape). Because the harmonics are simple integer multiples of the fundamental harmonic frequency (3x, 5x etc) it is simple to calculate how they combine to create an overall wave, or timbre. You simply move along the timeline, adding together the positive (compression) and negative (rarefaction) values of the waves at regular intervals.
Harmonics in a complex (square wave) electronically created (oscillators) sound
Sample MP3
Fundamental / 1st harmonic
In a complex sound, the vibration with the highest amplitude (the loudest) and lowest frequency (bassiest) is known as the fundamental. It is also known as the 1st harmonic.
Subsequent harmonics
Additional harmonics, each with a successively lower amplitude and higher frequency, will be named the 2nd, 3rd, 4th, etc harmonics. Higher harmonics are often referred to as "overtones" by musicians.
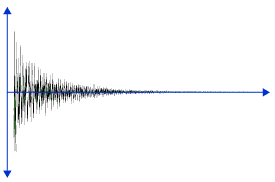
1) A single snare hit
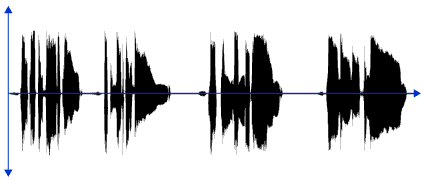
2) A lead vocal recording (2 bars)
Timbre
Oscillators apart, every sound source has a unique pattern of vibration. The unique relationship of its fundamental and subsequent harmonics create the unique character of the sound, which is known as its timbre.
Natural sounds sources produce enormously complex timbres made from many hundreds or thousands of individual harmonics. No matter how many harmonics a sound comprises, they are all represented by one single pattern of compression and rarefaction, a single wave of energy.
Overall frequency / pitch
Sounds which have a definite pitch are distinguished by a repetitive waveform. So a single sine wave vbrating at a constant frequency will have pitch.
Although complex waves are made from harmonics at many frequencies they can have an overall frequency or pitch too. This is true of musical instruments and singers (who can sing in tune!). This overall frequency is usually determined by the frequency of the fundamental or 1st harmonic.
