NOTE: Make sure you are familiar with basic sound theory before reading this article.
You may also wish to read ... What is an audio analogue to digital converter?
Join the dot pictures
Remember join-the-dot pictures? To produce a good image you must have sufficient dots to capture the detail of the shape AND the dots must be positioned accurately.
Quality in a join-the-dots picture depends on ...
- Number of dots
- Accuracy of the positioning of the dots
Image quality
All image designers know that quality of an image depends on 2 factors also ...
- Number of pixels per inch (ppi resolution)
- Number of colours in the images palette (determined by word length)
Creating a good quality digital audio signal depends on 2 similar parameters.
The 2 essential parameters
There are 2 important parameters which control the quality of the audio conversion process. These are ...
- Sample rate (number of measurements of amplitude per second). Sample rate is to audio what ppi or dpi is to images.
- Word length (accuracy of each measurement of amplitude). Word length in images determines the number of possible colours a pixel can be.
1. What is a sample?
Although it is common to use the word "sample" to refer to a complete sound (perhaps a piano note or drum break/loop), in digital theory ...
- a "sample" is a single measurement of amplitude.
A sample may also be referred to as a ...
- Snapshot
- Sample measurement
Amplitude measurement (sample or snapshot)
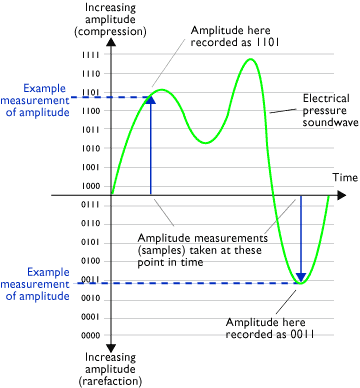
What is sample rate?
Sample rate is simply the number of samples (or measurements of amplitude) taken per second.
Sample rate is also known as ...
- Sample frequency. CD quality sample rate (for example) is expressed as "44.1KHz", meaning simply that the converter takes 44,100 measurements of amplitude per second. Sample frequency is independent of the frequency(s) of the soundwaves being converted.
- Sample bandwidth.
IMPORTANT NOTE: DO NOT confuse "Sample Frequency" with "Audio Frequency". Sample frequency is independent of the frequency(s) of the soundwaves being converted.
Sampling in a 4-bit converter
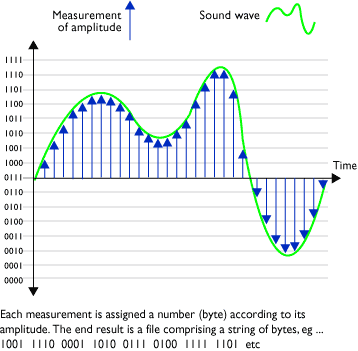
Sample rate is constant
Once set, sample rate does not vary during a recording, although different audio files recorded at different sample rates may be used together in a multitrack system if the software permits it. Usually, as in the case of a DAW, audio files of differing sample rates will need to conform (be converted too) a single sample rate, typically 44.1KHz, 48KHz, 96KHz or 192KHz. This sample rate is usually set in the application preferences for the recording session.
- Higher sample rates produce better quality recordings but also bigger file sizes which demand greater space on storage devices (such as hard drives), and faster processors (CPUs) to manipulate.
- Lower sample rates produce poorer quality but also smaller file sizes which demand less of storage systems, CPUs and will transfer over networks (internet) faster.
Example sample rates
Here are some commonly used sample rates.
| Format | Sample rate |
|---|---|
| Audio CD | 44,100 samples per second (44.1KHz) |
| DVD | Up to 96,000 (96KHz) |
| Professional multi-track recording (Logic Pro, ProTools) | 48KHz or 96KHz, and even sometimes 192KHz |
| MP3s | Variety of sample rates. The trade-off is always between quality and file size. |
Nyquist theory
During his research into digital audio in the first half of the 20th century, Harry Nyquist (a scientist) produced a simple rule that should be followed to determine appropriate sample rates for differing sounds.
"The sample rate should be a little over twice the amount of the highest audio frequency (harmonic) to be recorded if poor sound quality is to be avoided".
Because humans can hear audio frequencies as high as 20KHz (20,000cps/Hz), a minimum sample rate of 44.1KHz (or 44,100 sample measurements a second) was decided upon ...
Human audio spectrum = 20Hz to 20,000Hz (20KHz) ... therefore ...
Highest audio frequency = 20,000Hz ... therefore ...
20,000 x 2 = 40,000 + "a little bit more" = 44,100 samples per second
At the time, 44.1KHz was considered the best compromise of quality and file size. Over the last 20 years, there has been much debate among audio engineers and designers over the importance of using higher samples rates. Although many can't hear the difference between 44.1 and 192KHz audio (myself included!), others claim they can and that because equipment can easily handle higher rates, why not use them? Given the the quality of much modern domestic audio equipment (iPods, car stereos, phones, digital TV, DAB radio etc) produces increasingly inferior sound, it is unlikely that many consumers will benefit anyway.
NOTE: Increasing the sample rate above 44.1KHz does not dramatically improve the sound. Increasing word length (see later) has a greater impact.
Diagram 1 - accurate sampling:
Sampling (A to D) at 44.1KHz of one 20Hz cycle (low bass)
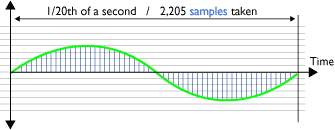
Diagram 2 - adequate sampling:
Sampling (A to D) at 44.1KHz of one 20,000Hz cycle (hi treble)
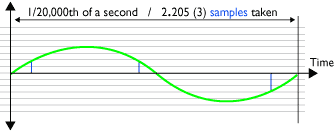
Diagram 3 - adequate playback:
Playback (A to D) at 44.1KHz of one 20,000Hz
cycle (hi treble)
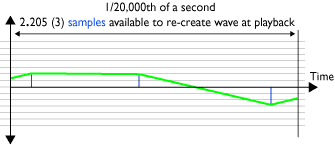
Diagram 4 - inadequate sampling:
Sampling (A to D) at 32KHz of two 20,000Hz cycles (hi treble)
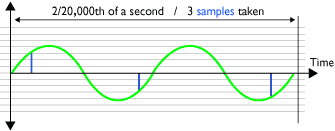
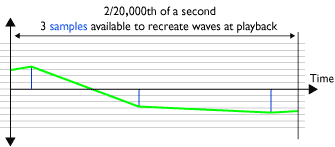
Diagram 5 - inadequate playback:
Playback (D to A) at 32KHz of two 20,000Hz cycles (hi treble)
Aliasing
If the sample rate is set too low (ie less than 2 times the highest audio frequency to be recorded), a type of distortion called "aliasing" will be audible in the signal when it is converted back to analogue by a DAC (digital to analogue converter).
Consider a soundwave/harmonic at a low frequency of 20Hz. There will be 20 cycles of its waveform every second. This means that if it is recorded at a sample rate of 44.1KHz, each cycle will be represented by 2,205 samples. 44,100 divided by 20 = 2,205. So each cycle of a low frequency soundwave/harmonic is measured comprehensively and the shape of the waveform is recorded accurately (Diagram 1).
Problems with hi-frequency soundwaves/harmonics
NOTE: Remember that once set, sample rate doesn't vary during the recording of a soundwave, no matter what frequencies/harmonics the wave contains.
Now consider a soundwave/harmonic at a high frequency of 20,000Hz (20kHz). There will be 20,000 cycles of its waveform every second. This means each cycle will be represented by 2.205 samples (Diagram 2). 44,100 divided by 20,000 = 2.205. So each cycle of a high frequency soundwave/harmonic is measured barely enough times to retain its basic shape. Its adequate but not very accurate.
When the digital data is converted back into an an analogue electrical soundwa
ve (Diagram 3) by a D to A converter at playback (in order to be sent to a monitoring system and heard), there will be just enough information to re-create the original wave but not very accurately. Filters are used to smooth the wave back into the best possible shape. This difference between the sampled and played back signal is heard as distortion.
Aliasing noise
There is an effect in film making caused by its fixed frame rate (24 frames per second) that can lead to the odd visible effect of a speeding cars wheels appearing to revolve backwards. This happens because 24fps is insufficient to capture fast motion. This is called (visual) aliasing.
In digital audio recording, if the recording sample rate is set lower than the required minimum 44.1kHz (for the high frequency soundwave/harmonics), then the soundwave produced by the D to A conversion at playback will be disastrously different. The wave is changed to a lower frequency wave.
In a complex soundwave containing many harmonics, only the harmonics for which the sample rate is insufficient will be altered. Harmonics for which the sample rate is adequate will reproduced accurately. The audible effect of this can be audible random noise or unpleasant and unwanted lower harmonics within the sound. The unwanted harmonics are known as Aliasing Noise.
Consider a soundwave at 20,000Hz being recorded at a sample rate of 32kHz. This would mean 1.5 samples per cycle of the waveform, clearly inadequate (Diagram 4).
Now look at the soundwave reconstructed by the D to A converter (Diagram 5). The wave shape has changed dramatically, the wave is a lower frequency, and the sound has been distorted.
Anti-aliasing filters
Analogue to digital converters therefore employ a low pass filter before the converters to remove any harmonics from the soundwave which are above the highest frequency that the sample rate can accommodate. Thus, an anti-aliasing filter in a CD recorder will remove any harmonics above 20KHz from a soundwave before it is converted and recorded.
Jitter
Jitter refers to irregularities in the time intervals between samples. Jitter can occur when ...
- the clock regulating the A to D conversion is not regular, this is the worse case scenario because jitter is "written" into the data stream
- a cable with (relatively) high capacitance, in which the samples (pulse wave) are traveling, adversely effects the wave shape
- the clock regulating the D to A conversion is not regular
Therefore the accuracy of the digital clock, which governs when samples occur, is paramount. If the clock is not accurate, jitter will occur and the audio quality will suffer.
As an example, consider a digital signal that has been created by a (theoretically) perfect A to D converter where each sample is taken at precisely consistent intervals. If that signal is later sent through a digital system whose clock is less accurate (causing the sample intervals to fluctuate), then the correct sample amplitudes may not occur at the right places, causing audible distortion.
What kind of distortion does jitter cause?
If the clock irregularities/timing errors are random, then so will the jitter and the resulting amplitude inaccuracies/distortion. Random distortion is noise. Because these timing errors are small and fast, they produce more amplitude distortion in the higher frequencies. The audible result is hiss.
2. What is audio word length?
Increasing sample rate will not always significantly improve sound quality. Increasing word length will result in a more obvious improvement in sound quality for most listeners.
Simply put ...
... in digital audio, word length determines the accuracy of each sample measurement. Better accuracy means less distortion which results in better sound!
Word length
In audio files, higher word length means better sound quality. In short, higher word lengths provide a converter with a more accurate "ruler" (higher bit resolution) to measure amplitude with, thereby producing more accurate measurements. In audio quality terms, more accurate measurements mean less distortion of the true shape of the soundwave.
| Word length | No of possible values |
|---|---|
| 4 | 16 |
| 8 | 256 |
| 16 | 65,536 |
Accuracy of amplitude measurement
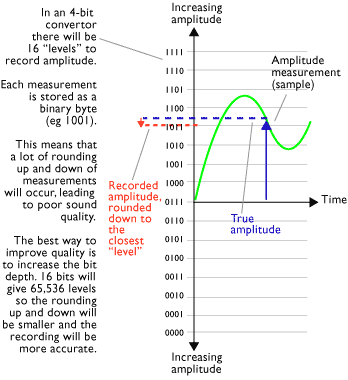
Example word lengths ... 8-bit
8-bit sampling system In an 8-bit A-to-D converter, each measurement is recorded as an 8-bit binary byte. Between 00000000 and 11111111 there are 256 possible values. (See computer counting systems). This means that each sample measurement of amplitude will be recorded as one of these numbers.
Quantisation
A "ruler" with 256 divisions, or "points of resolution", is NOT very accurate. If when a measurement is taken, the amplitude of the wave does not fall exactly on one of these points, then the measurement must be rounded up or down to the next nearest point. This process is called Quantisation and results in a distorted recording of the true shape of the wave.
A measurement which has been rounded up or down is known as a quantisation error and produces quantisation distortion. At loud signal levels quantisation errors manifests themselves as noise (similar to analogue noise), but at low signal levels they can manifest themselves as unwanted audible distortion.
The effects of quantisation errors are most apparent at lower word lengths. Higher word lengths increase the quality of sound but also the quantity of data and therefore file sizes. 16 bit bytes are of course twice as big as 8 bit bytes. CD quality sound requires 5Mb of storage space for 1 mono minute (10Mb for a stereo minute).
Here are some simple rules ...
- The longer the word length the larger the file size,the smaller the quantisation errors, the less the distortion, the better quality the sound
- The shorter the word length, the smaller the file size, the larger the quantisation errors, the more the distortion, the poorer quality the sound
16 & 24 word length
CD quality is 44.1KHz / 16-bit. This means that every second a converter will produce 44,100 16 bit numbers.
44.1KHz / 24-bit recordings are higher quality than 44.1KHz / 16-bit recordings. Of course the sound files are bigger, but in general, current computer CPU power, installed RAM memory and hard disc size can handle them. Many sound engineers are now using 24-bit as standard even though the finished mixes must be converted to 16-bit prior to audio CD duplication.
It is generally agreed that a 44.1Khz / 24-bit recordings sound superior to those made at 96KHz / 16 bit.
Recording at too low a level
It is important to recognise that even if a converter has a high word length, setting the record level too low will result in a smaller range of bits being used and effectively reduce the word length of the recording.
Setting the record level too high however, will risk digital clipping, an unpleasant distortion that is the result of all sample measurements that exceed the upper limit of the word length range of the system being quantised down to the highest available value. For example, in a 16-bit system this might be 1111111111111111. Picture a mountain with its peak sliced off.
It is therefore important that recordings are made at the highest possible level without clipping, which explains why the signal is often passed through an audio limiter before it enters the A to D converter.
Audio dithering
The process of converting a long word length audio signal to a shorter one is most commonly referred to as truncating. Essentially some of the bits in each byte/sample are thrown away (the least significant bits to be precise).
| 24 bit byte/sample before truncating | 16 bit byte/sample after truncating |
|---|---|
| 100101110100010111100001 | 1001011101000101 (11100001 has been removed) |
The effect of this process on an audio signal is to "magnify" quantisation errors which can result in audible distortion, especially in the quieter parts of an audio signal.
Audio dithering is a process whereby low level white noise (random sound) is introduced into the signal to help randomise quantisation errors. The effect of this is to turn the audible effects of quantisation errors from unpleasant distortion into a the more acceptable analogue noise.
Dithering is most commonly used at the CD mastering stage of music production, but dither can be used for other reasons too. The following are some of the processes that involve dithering ...
Creating a red book audio compliant audio file
If you have created a 24-bit / 44.1KHz audio mix master of a recording in your DAW, and you want to create an audio CD, it will need to be converted to 16-bit in order to conform to the red book audio CD standard. During the conversion process you use a dithering algorithm to minimise the increase in distortion that will result from the "enlargement" of existing quantisation errors.
Digital interconnection
When passing a signal digitally between two devices, such as a DAW and a digital mixer, the signal may be converted and dithered if the word lengths of the two systems don't match (the sample rate must match, otherwise a sample rate converter will need to be used).
Digital processors
Some effect processors allow you to set parameters for dither which will be automatically be introduced in the signal if it drops below a certain level.
Analogue to digital conversion
Many A to D converters automatically dither as part of the sampling process, and applications and software which allow downsampling or word length conversion often give the user the option to introduce dither and to control the amount of dither.

